Inlämningsuppgift 3 - John Croft 19930814-7959

Contents

3.1 Bestämning av processens överföringsfunktion utifrån dess stegsvar

Stegsvaret för processen har översväng och måste därmed ha komplexa rötter i överföringsfunktionens nämnare. För att bestämma överföringsfunktionen kan man då tillämpa den metoden och formler som beskrivs i [1]. Metoden kräver att man utläser följande parametrar manuellt ur processens stegsvar: storleken på första översvängen, a, storleken på andra översvängen, b, periodtiden för svängningarna, 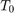$$ T_0 $$ och den statiska förstärkningen, $$ K_0 $$.

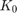a = 0.82;
b = 0.5;
k = 1;
T0 = 4;

Därefter kan parametrarna d, 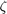$$ \zeta $$ ('zeta' i kod) och 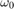$$ \omega_0 $$ ('w0' i kod) bestämmas.

d = b/a

zeta = 1/(sqrt(((2*pi) / log(d))^2 + 1) )
w0 = (2*pi)/(T0*sqrt(1 - zeta^2 ))

d =

    0.6098


zeta =

    0.0785


w0 =

    1.5757

Processens överföringsfunktion kan nu beräknas och ritas med följande formel: 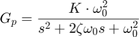$$ G_p = \frac{K \cdot \omega_{0}^{2}}{s^2 + 2 \zeta \omega_{0} s + \omega_{0}^{2} } $$

s=tf('s');
Gp = (k*w0^2)/(s^2 + 2*zeta*w0*s + w0^2 )

step(Gp)
ylim([0 2])
xlim([0 12])
grid on
yticks([0 1/3 2/3 1 4/3 5/3 2])

Gp =
 
          2.483
  ----------------------
  s^2 + 0.2473 s + 2.483
 
Continuous-time transfer function.

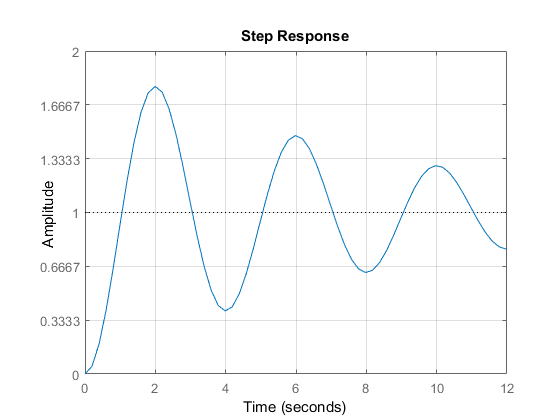
Om man jämför med det orginala stegsvaret så ser man att den beräknade överföringsfunktionen stämmer ganska exakt.


Published with MATLAB® R2016b